| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 미드시청
- leetcode
- 사이드
- 30분
- FIT XR
- Daily Challenge
- 3줄정리
- 만화도
- Problem Solving
- realclass
- 월간
- 스탭퍼
- 파비최
- 잡생각
- 영어공부
- 운동
- 개발자
- 프로젝트
- 매일
- 읽기
- 영어원서읽기
- 괜찮음
- 화상영어
- Writing
- 쓰릴오브파이트
- English
- 10분
- 리얼 클래스
- 링피트
- 뭐든
- Today
- Total
파비의 매일매일 공부기록
[Week of DP] BOJ 1309 #2 본문
풀이에는 아래의 두 블로그의 글을 참조했다.
wookje.dance/2017/08/05/boj-1309-%EB%8F%99%EB%AC%BC%EC%9B%90/
역시나 해설을 보면 매우 쉬운 문제였다는걸 알 수 있다....
근데 일부 해설이 내가 이해하기에는 조금 이상한거 같아서 하나씩 다시 따져봤다.
일단 2가지 Case로 분류를 해야한다.
가장 상단에서부터 사자를 넣는다고 가정했을 때,
1. 마지막 줄에 사자를 넣지 않는 경우
2. 마지막 줄의 왼쪽에 사자를 넣는 경우 or 마지막 줄의 오른쪽에 사자를 넣는 경우
사실 2번째 Case는 2개로 나눌수 있는데,
어짜피 경우의 수라서 2개의 경우를 1개로 합쳐놨다.
n이 0인 경우에는(우리가 0개줄 - 없는 경우)
1번 케이스는 존재하므로 1
2번 케이스는 존재하지 않으므로 0 + 0 = 0
그러므로 dp[0] = 1이 된다.
n이 1인 경우에는(우리가 1개줄)
1번 케이스는 1가지 존재
2번 케이스는 왼쪽에 넣는 경우 1 + 오른쪽에 넣는 경우 1로 총 2가지 존재
그러므로 dp[1] = 3이 된다.
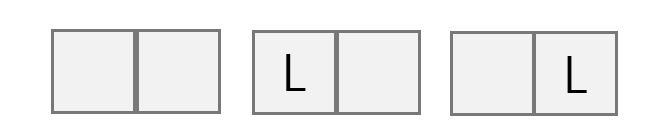
n이 2인 경우에는(우리가 2개줄)
1번 케이스는
- 사자가 아예 없는 경우 1
- 1번째 줄 왼쪽에 사자 있음, 2번째 줄에 사자 없는 경우 1
- 1번째 줄 오른쪽에 사자 있음, 2번째 줄에 사자 없는 경우 1
총 3가지 존재
2번 케이스는
- 1번째 줄에 사자 없음, 2번째 줄 왼쪽에 사자 있는 경우 1
- 1번째 줄 오른쪽에 사자 있음, 2번째 줄 왼쪽에 사자 있는 경우 1
- 1번째 줄에 사자 없음, 2번째 줄 오른쪽에 사자 있는 경우 1
- 1번째 줄 왼쪽에 사자 있음, 2번째 줄 오른쪽에 사자 있는 경우 1
그러므로 dp[2] = 7이 된다.

n이 3인 경우에는(우리가 3개줄)
1번 케이스는
- n이 2인 경우의 전체 경우 7
2번 케이스는
- n이 2인 경우중 1번 케이스 * 2로 6개
> n이 2인 경우중 1번 케이스는 3번째 줄 왼쪽, 오른쪽 둘다 들어갈 수 있으므로 곱하기 2를 해줌
- n이 2인 경우중 2번 케이스 4개
> n이 2인 경우중 2번 케이스는 왼쪽만 들어갈수 있거나, 오른쪽만 들어갈수 있기 때문에 4가 됨
그러므로 dp[3] = 17이 된다.

이렇게 그려보고 보니
1번 케이스는 n-1의 전체 갯수와 동일하고 dc1[n] = dc1[n-1] + dc2[n-1]
2번 케이스는 (n-1의 1번 케이스) * 2 + n-1의 2번 케이스와 동일하다. dc2[n] = dc1[n-1] * 2 + dc2[n-1]
d[n] = dc1[n] + dc2[n] 이 되며, 계산시 항상 9901을 mod 한 연산을 해주어야 한다.
위에 정리한 내용을 그대로 소스로 적으면 아래와 같다.
if __name__ == "__main__":
n = int(input())
mod_n = 9901
d = [0 for _ in range(n + 1)]
dc1 = [1 for _ in range(n + 1)]
dc2 = [0 for _ in range(n + 1)]
for i in range(1, n + 1):
dc1[i] = (dc1[i - 1] + dc2[i - 1]) % mod_n
dc2[i] = (2 * dc1[i - 1] + dc2[i - 1]) % mod_n
d[i] = (dc1[i] + dc2[i]) % mod_n
print(d[n])dc1과 dc2를 하나로 합쳐서 수식으로 정리해서 풀수도 있지만
굳이 그렇게 할 필요는 없을 것같아서 여기서 마무리 짓도록 하겠다.
'Problem Solving > BOJ' 카테고리의 다른 글
| [Week of DP] BOJ 11660 #1 (2) | 2021.01.08 |
|---|---|
| [Week of DP] BOJ 1495 (4) | 2021.01.03 |
| [Week of DP] BOJ 1309 #1 (0) | 2020.12.24 |
| [Week of DP] BOJ 2294 #2 (0) | 2020.12.19 |
| [Week of DP] BOJ 2294 #1 (0) | 2020.12.16 |